毎年10万円ずつを20年間積み立てた場合、20年後の金額は200万円になります。
しかし、積み立てたお金を年利3%で運用していた場合、20年後の金額はどうなるでしょうか？
普通に計算しようとすると少し面倒ですが、”ある係数”を使えば簡単に計算することができます。
今回は上記のような資金計画を立てる際に役に立つ6つの係数についてご紹介します。
お金の現在価値と将来価値
同じ「100万円」でも、現在と将来ではその価値は異なります。
例えば、今持っている100万円を年利5%で3年間運用した場合、3年後の金額は115.8万円になります。
つまり、現在の100万円の価値は3年後の115.8万円と同じであるということです。
このように、今のお金の価値を将来の価値に換算したり、逆に将来のお金の価値を今の価値に換算したりすることは、将来に備えて資金計画を立てる上で重要なステップです。
この計算は、次に説明する「6つの係数」を活用することで簡単に行うことができるようになります。
6つの係数
資金計画に役立つ係数には、以下の6つがあります。
- 終価係数
- 現価係数
- 年金終価係数
- 減債基金係数
- 資本回収係数
- 年金現価係数
年利率3%・5年間の場合、各係数は以下のようになります。
| 係数 | 年利率3%・5年間 |
|---|---|
| 終価係数 | 1.159 |
| 現価係数 | 0.863 |
| 年金終価係数 | 5.309 |
| 減債基金係数 | 0.188 |
| 資本回収係数 | 0.218 |
| 年金現価係数 | 4.580 |
その他の利率・期間の係数については、カシオ計算機(株)様の「Keisan」というサイトで求めることができますので、下記リンクからご自身の条件に合った係数をご確認ください。
それでは、それぞれの係数が具体的にどのような場面で活用されるかについて解説していきます。
終価係数
終価係数は、今のお金は「将来いくら？」を計算します。
100万円を年利3%で運用した場合、5年後の金額はいくら？
年利3%・5年間の終価係数は1.159なので、
100万円×1.159を計算すると、5年後の金額は115.9万円になります。
現価係数
現価係数は、将来のお金は「今いくら？」を計算します。
年利3%で５年後に100万円を用意する場合、必要な元本はいくら？
年利3%・5年間の現価係数は0.863なので、
100万円×0.863を計算すると、必要な元本は86.3万円になります。
年金終価係数
年金終価係数は、毎年貯めたお金は「将来いくら？」を計算します。
年利3%で毎年20万円ずつ５年間積み立てた場合、5年後の金額はいくら？
年利3%・5年間の年金終価係数は5.309なので、
20万円×5.309を計算すると、5年後の金額は106.18万円になります。
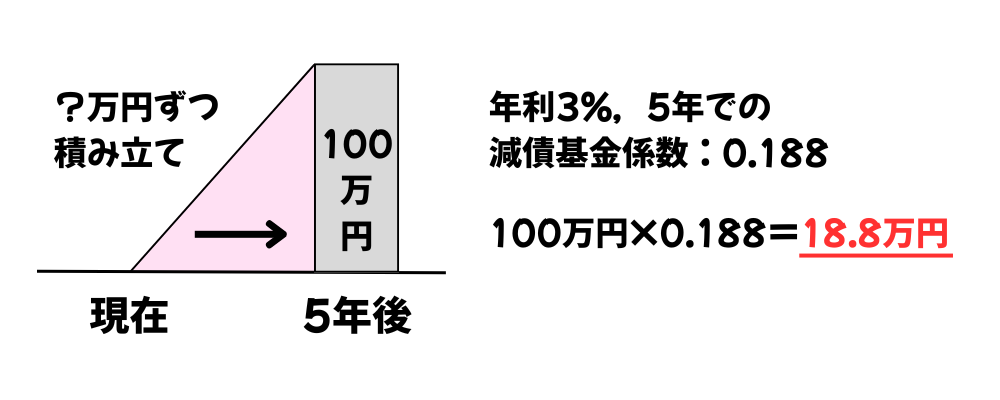
減債基金係数
減債基金係数は、将来の目標金額を貯めるために必要なのは「毎年いくら？」を計算します。
年利3%で５年後に100万円を用意する場合、毎年の積立額はいくら？
年利3%・5年間の減債基金係数は0.188なので、
100万円×0.188を計算すると、毎年の積立額は18.8万円になります。
資本回収係数
資本回収係数は、今のお金を一定額ずつ取り崩す場合の受取額は「毎年いくら？」を計算します。
100万円を年利3%で運用しながら５年間で取り崩す場合、毎年の受取額はいくら？
年利3%・5年間の減債基金係数は0.218なので、
100万円×0.218を計算すると、毎年の受取額は21.8万円になります。
また、資本回収係数はローンの支払額を計算する際にも利用できます。
100万円の借入金額を年利3%・５年間で返済する場合、上記の計算から毎年の返済額は21.8万円と求めることができます。
年金現価係数
年金現価係数は、今のお金を一定額ずつ取り崩す場合に必要な「元本はいくら？」を計算します。
年利3%で運用しながら毎年20万円ずつ５年間にわたって受け取る場合、必要な元本はいくら？
年利3%・5年間の年金現価係数は4.580なので、
20万円×0.4580を計算すると、必要な元本は91.6万円になります。
まとめ
今回は資金計画に役立つ6つの係数についてご紹介しました。
どんな時にどの係数を使えば良いか、初めは難しく感じるかもしれません。
しかし、6つの係数をうまく活用できれば、資金計画をスムーズに立てられるようになります。
例題を参考にしながら各係数の使い方をマスターしてくださいね。
