今回は、以前ご紹介した資産形成に役立つ6つの係数を活用して、実際に身近な事例で資金計画を立ててみましょう。
6つの係数について詳しく知りたい方は、先にこちらの記事をご覧ください。
6つの係数
今回の記事内で使用する6つの係数の値は、リプレックス(株)様の「Keisan」のサイトから引用しております。

老後資金の計画
まずはAさんの事例です。

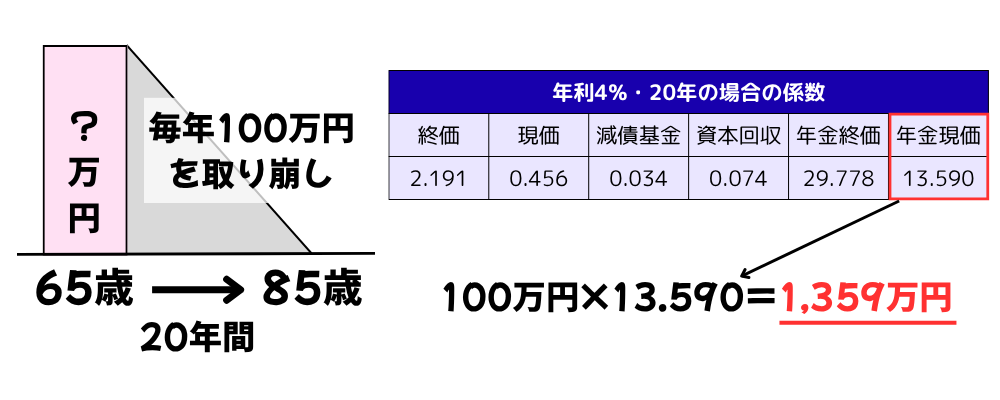
老後の65歳~85歳までの20年間に渡って、資金を年利4%で運用しながら毎年100万円を取り崩したい。そのためには65歳の時点でいくら必要?
毎年一定額を取り崩す際に必要な元本を求めるときには「年金現価係数」を使用します。
年利4%・20年の年金現価係数は13.590なので、
100万円×13.590を計算すると、65歳時点で必要な金額は1,359万円になります。
ローンの計画
次に、Bさんの事例です。

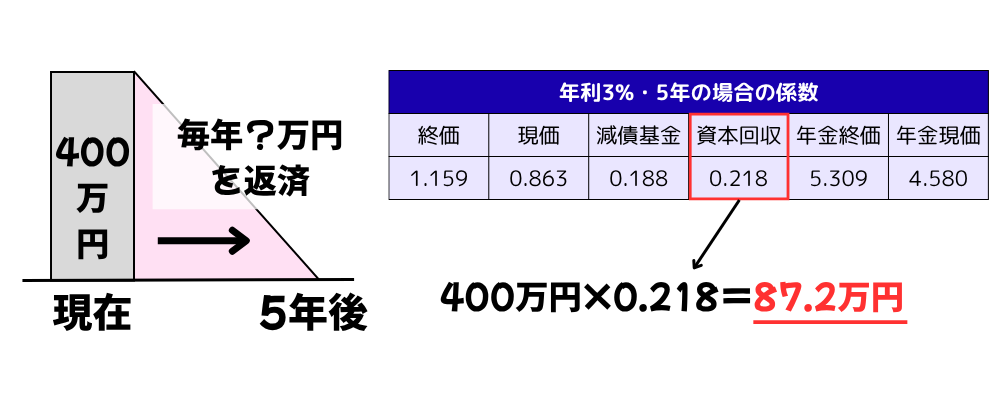
総額400万円の車を全額ローン支払いで購入する予定。金利が年3%、借入期間が5年の場合、毎年の返済額はいくら?
ローンを組む際の毎年の支払い額を求めるときには「資本回収係数」を使用します。
年利3%・5年の資本回収係数は0.218なので、
400万円×0.218を計算すると、毎年の返済金額は87.2万円になります。
教育資金の計画
最後にCさんの事例です。

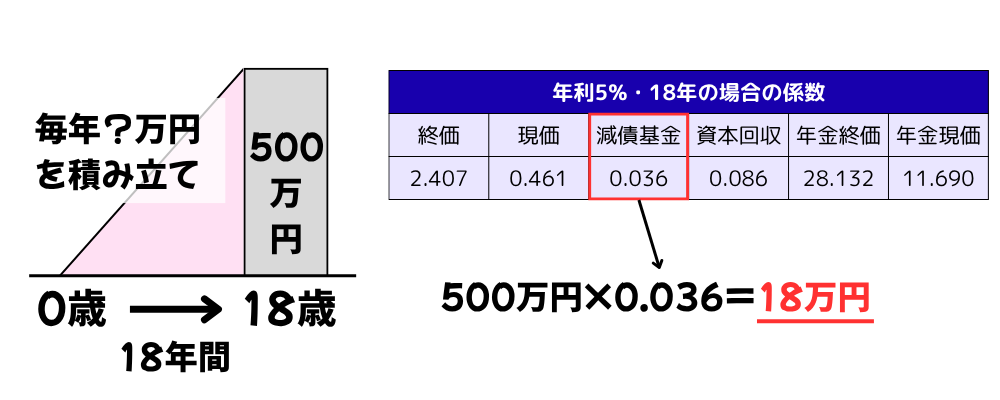
今年生まれた子どもの大学への進学費用として今から18年間で500万円を準備したい。年利5%で運用しながら積み立てをする場合、毎年の積立額はいくら必要?
毎年の積立額を求めるときには「減債基金係数」を使用します。
年利5%・18年の減債基金係数は0.036なので、
500万円×0.036を計算すると、毎年の積立金額は18万円になります。
まとめ
6つの係数については、FP試験の対策として勉強する方が多いと思いますが、単なる試験対策として終わらせてしまうのは非常にもったいないです。
今回の事例を参考に、6つの係数を活用してご自身の資金計画を立ててみましょう!




